728x90
트리 순회
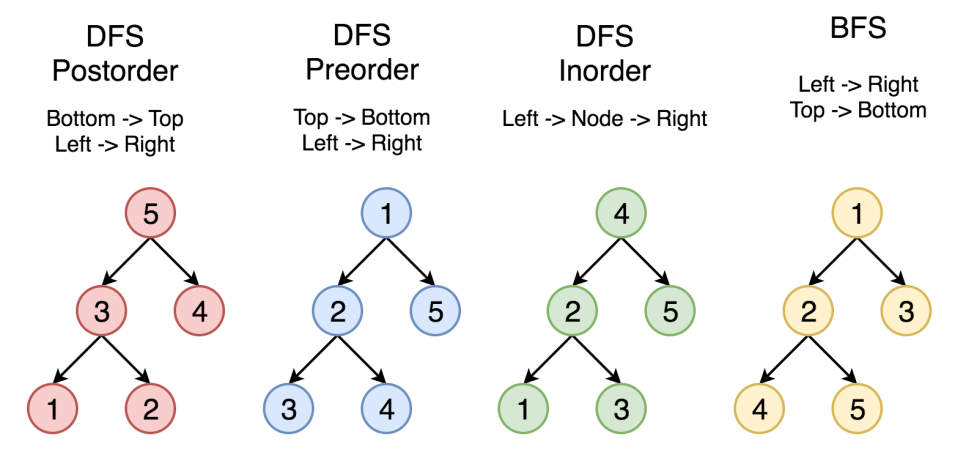
트리 순회(Tree traversal)는 트리 구조에서 각각의 노드를 정확히 한 번만, 체계적인 방법으로 방문하는 과정을 말한다. 이는 노드를 방문하는 순서에 따라 후위 순회, 전위 순회, 중위 순회, 레벨 순회가 있다. 보통 설명할 때는 이진 트리를 기반으로 설명하지만 다른 모든 트리에서 일반화를 시킬 수 있다.
후위 순회
후위 순회(postorder traversal)는 자식들 노드를 방문하고 자신의 노드를 방문하는 것을 말한다.
postorder( node )
if (node.visited == false)
postorder( node->left )
postorder( node->right )
node.visited = true
전위 순회
전위 순회(preorder traversal)는 먼저 자신의 노드를 방문하고 그 다음 노드들을 방문하는 것을 말한다. (DFS)
preorder( node )
if (node.visited == false)
node.visited = true
preorder( node->left )
preorder( node->right )
중위 순회
중위 순회(inorder traversal)는 왼쪽 노드를 먼저 방문 그 다음의 자신의 노드를 방문하고 그 다음 오른쪽 노드를 방문하는 것을 말한다.
inorder( node )
if (node.visited == false)
inorder( node->left )
node.visited = true
inorder( node->right )
레벨 순회
레벨 순회(lever traversal)는 BFS
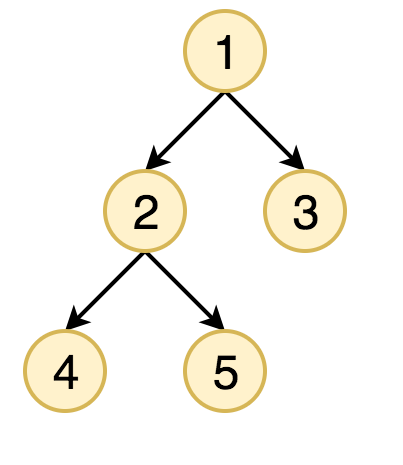
Q. 아래의 그래프가 주어졌을 때 preorder, inorder, postorder를 구현하라.
adj = [[] for _ in range(1004)]
visited = [0] * 1004
def postOrder(here):
if visited[here] == 0:
if len(adj[here]) == 1:
postOrder(adj[here][0])
if len(adj[here]) == 2:
postOrder(adj[here][0])
postOrder(adj[here][1])
visited[here] = 1
print(here, end=' ')
def preOrder(here):
if visited[here] == 0:
visited[here] = 1
print(here, end=' ')
if len(adj[here]) == 1:
preOrder(adj[here][0])
if len(adj[here]) == 2:
preOrder(adj[here][0])
preOrder(adj[here][1])
def inOrder(here):
if visited[here] == 0:
if len(adj[here]) == 1:
inOrder(adj[here][0])
visited[here] = 1
print(here, end=' ')
elif len(adj[here]) == 2:
inOrder(adj[here][0])
visited[here] = 1
print(here, end=' ')
inOrder(adj[here][1])
else:
visited[here] = 1
print(here, end=' ')
adj[1].extend([2, 3])
adj[2].extend([4, 5])
root = 1
print("\n트리순회 : postOrder")
postOrder(root)
visited = [0] * 1004 # Reset visited array
print("\n트리순회 : preOrder")
preOrder(root)
visited = [0] * 1004 # Reset visited array
print("\n트리순회 : inOrder")
inOrder(root)
'''
트리순회 : postOrder
4 5 2 3 1
트리순회 : preOrder
1 2 4 5 3
트리순회 : inOrder
4 2 5 1 3
'''
728x90
'☢️ CT' 카테고리의 다른 글
| 개념 #11. DFS와 BFS 비교 (0) | 2023.07.29 |
|---|---|
| 개념 #10. 너비 우선 탐색(BFS, Breadth First Search) (0) | 2023.07.14 |
| 개념 #9. 깊이 우선 탐색(DFS, Depth First Search) (0) | 2023.07.14 |
| 개념 #8. 연결된 컴포넌트(connected component) (0) | 2023.07.14 |
| 개념 #7. 맵과 방향 벡터(direction vector) (0) | 2023.07.14 |
